10進法は 0,1,2,3、4,5,6,7,8,9 と10個の数字を使います。
2進法は 0,1 の2個の数字を使います。
16進法は 0,1,2、…、8,9、A、B、C、D、E,F と0から9までの数字と、AからFの記号を11から15の数字に見立て、16個の数字を使います。
手の指を使って32通りの順番を持った、状態を表現でき、それを数字として読めれば32個の数字を使えることになります。しかも、1本1本の指が2進数の一桁になっているので、この特徴を使えば、手早く2進数に変換できるはずです。
手を使って2進数に手早く変換する方法
32進法は、1けたが32なので、一つ上の桁はその32倍になります。
桁数は手の数になります。
一番下の桁の重みは32の0乗で 1
次の桁は 32の1乗で 32
次の桁は 32の2乗で 1024
次の桁は 32の3条で 32768
となります。
つまり、手が4本あれば 0から32767まで表現できます。
では 2019 を2進数に変換すると
2019 ÷ 1024 = 1 余り 995
商が 1 なので 手を1本使って

つぎに 余りの 995を
995 ÷ 32 = 31 余り 3
商が31なので 次の手は

余りが 3 なので
次の手は

この3本の手を使って
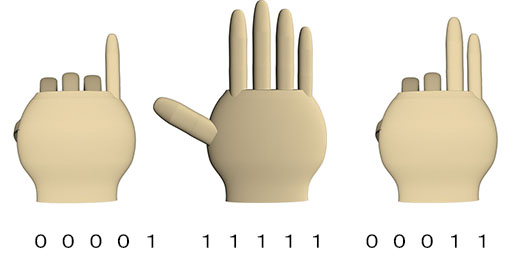
2019を2進数で表すと
000011111100011 となります。
はたして便利でしょうか?
32通りの記号を覚えるのは大変ですが、手の形なら何とかなりそうです。また、記号をすぐに数値にできるかが問題ですが、もともと手の指は2進数を現しているので、そのまま数字と言えます。ちょっと面白そうなのでやってみましたが、便利かどうかは今のところ不明です。
